Hidden Markov Model
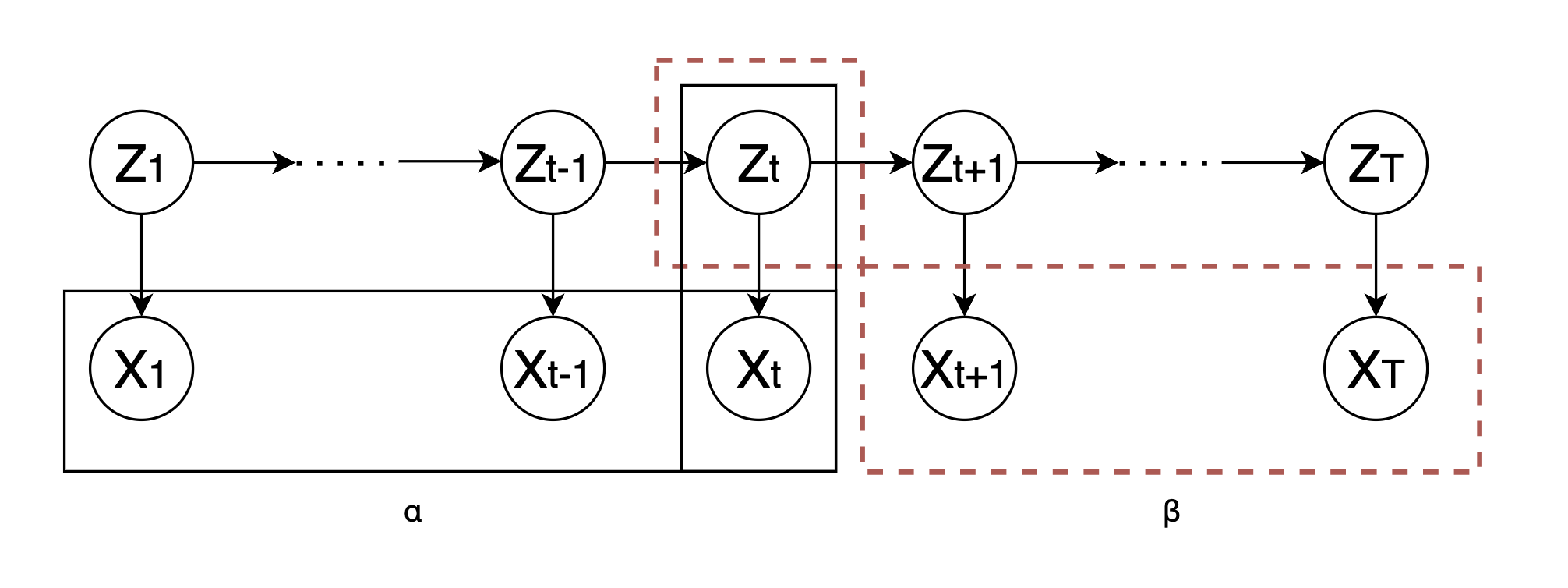
Basics of model
\[ \lambda=(\pi,\mathcal A,\mathcal B) \]
\(\pi:\) initial distribution
\(\mathcal A:\) state-transition matrix
\(\mathcal B:\) emission matrix
\(\alpha_t=P(X_1,\cdots,X_t,Z_t)\)
\(\beta_t=P(X_{t+1},\cdots,X_T|Z_t)\)
Assumption
- Homogeneous Markov Assumption
\[ P(Z_{t+1}|Z_t,\cdots,Z_1,X_t,\cdots,X_1)=P(Z_{t+1}|Z_t) \]
- Independent observations Assumption
\[ P(X_t|Z_t,\cdots,Z_1,X_t,\cdots,X_1)=P(X_t|Z_t) \]
Tasks
\[ \begin{cases} \text{Learning}\,(\lambda:\text{unknown})\quad\lambda_{MLE}=\underset{\lambda} {\operatorname{arg\,max}}P(X|\lambda)\quad \text{[Baum–Welch Algorithm]}\\ \text{Inference}\,(\lambda:\text{known}) \begin{cases} \text{Decoding}: Z=\underset{Z} {\operatorname{arg\,max}}P(Z|X)\quad \text{[Viterbi Algorithm]}\\ \text{Prob of evidence}:P(X) \quad \text{[Forward Algorithm] | [Backward Algorithm]}\\ \text{Filtering(online)}:P(Z_t|X_1,\cdots\,X_t) \quad \text{[Forward Algorithm]}\\ \text{Smoothing(offline)}:P(Z_t|X_1,\cdots\,X_T) \quad \text{[Forward-Backward Algorithm]}\\ \text{Prediction}:P(Z_{t+1}|X_1,\cdots\,X_t) \text{ or } P(X_{t+1}|X_1,\cdots\,X_t)\quad \text{[Forward Algorithm]}\\ \end{cases} \end{cases} \]